Giải SBT Toán 8 Bài 4: Đường trung bình của tam giác, của hình thang

Bài 40 trang 84 SBT Toán 8 Tập 1: Cho tam giác ABC, các đường trung tuyến BD, CE. Gọi M, N theo thứ tự là trung điểm của BE, CD. Gọi I, K theo thứ tự là giao điểm của MN với BD, CE. Chứng minh MI = IK = KN.

Lời giải:

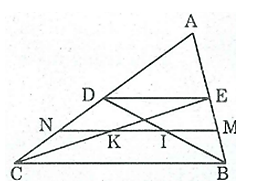
Trong ΔABC ta có: E là trung điểm của cạnh AB;

D là trung điểm của cạnh AC;

Nên ED là đường trung bình của Δ ABC.

⇒ ED // BC và ED = 12BC.

(tính chất đường trung bình của tam giác)

+) Tứ giác BCDE có ED // BC nên BCDE là hình thang.

Trong hình thang BCDE, ta có: BC // DE

M là trung điểm cạnh bên BE

N là trung điểm cạnh bên CD

Nên MN là đường trung hình hình thang BCDE

⇒ MN // DE

MN​ = DE​  +  BC​​2  =  BC2​​ +​​BC​2  =  3BC4

(tính chất đường trung bình hình thang)

Trong ΔBED, ta có: M là trung điểm BE và MI // DE nên MI đi qua trung điểm của BD do đó I là trung điểm của BD

Suy ra: MI là đường trung bình của ΔBED

⇒ MI = 12DE = 14BC (tính chất đường trung bình của tam giác)

Trong ΔCED ta có: N là trung điểm CD và NK // DE nên NK đi qua trung điểm của CE do đó K là trung điểm của CE.

Suy ra: NK là đường trung bình của ΔCED.

⇒ NK =12 DE = 14BC (tính chất đường trung bình của tam giác)

IK = MN – (MI + NK)

= 34BC – ( 14BC + 14BC)

= 14BC

⇒ MI = IK = KN = 14BC.