Giải Toán 10 Bài 3: Dấu của nhị thức bậc nhất
Video Giải Bài 2 trang 94 Toán lớp 10 Đại số
Bài 2 trang 94 Toán lớp 10 Đại số: Giải các bất phương trình
a) 2x−1≤52x−1;
b) 1x+1<1x−12;
c) 1x+2x+4<3x+3;
d) x2−3x+1x2−1<1.
Lời giải:
a)
+ Điều kiện:
x−1≠02x−1≠0⇔x≠1x≠12
+ Ta có:
2x−1≤52x−1⇔2x−1−52x−1≤0
⇔22x−1−5x−1x−12x−1≤0
(adsbygoogle=window.adsbygoogle||[]).push({})⇔4x−2−5x+5x−12x−1≤0
⇔−x+3x−12x−1≤0
+ Đặt f(x) = −x+3x−12x−1
Suy ra f(x) = 0 khi –x + 3 = 0 hay x = 3.
+ Ta lập bảng xét dấu:
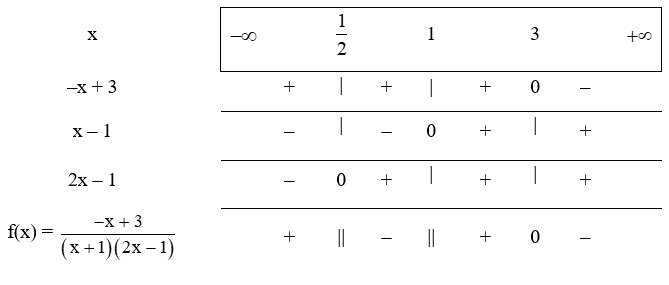
Vậy tập nghiệm của bất phương trình là S=12;1∪3;+∞
b)
+ Điều kiện: x+1≠0x−1≠0⇒x≠−1x≠1
+ Ta có:
1x+1<1(x−1)2⇔1x+1−1(x−1)2<0
⇔(x−1)2−(x+1)(x+1)(x−1)2<0
⇔x2−2x+1−x−1(x+1)(x−1)2<0
⇔x2−3x(x+1)(x−1)2<0
⇔x(x−3)(x+1)(x−1)2<0
+ Đặt f(x)=x(x−3)(x+1)(x−1)2
Suy ra f(x) = 0 khi x = 0 hoặc x = 3
+ Ta có bảng xét dấu:
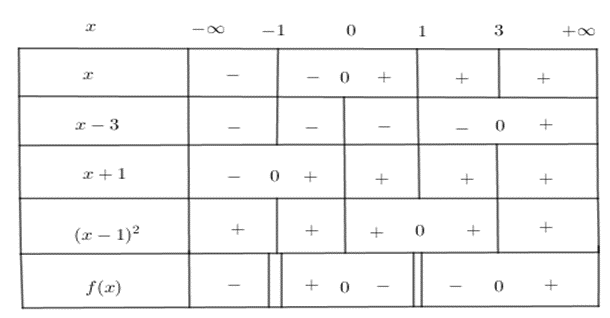
Vậy tập nghiệm của bất phương trình là S=−∞;−1∪0;1∪1;3
c)
+ Điều kiện: x≠0x+4≠0x+3≠0⇔x≠0x≠−4x≠−3
+ Ta có:
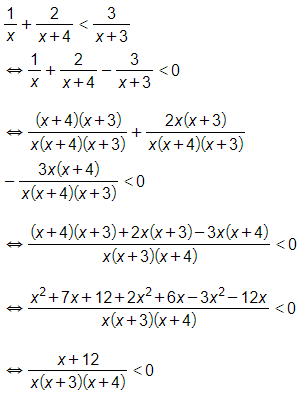
+ Đặt f(x)=x+12x(x+3)(x+4)
Suy ra f(x) = 0 khi x + 12 = 0 hay x = –12.
+ Ta có bảng xét dấu:
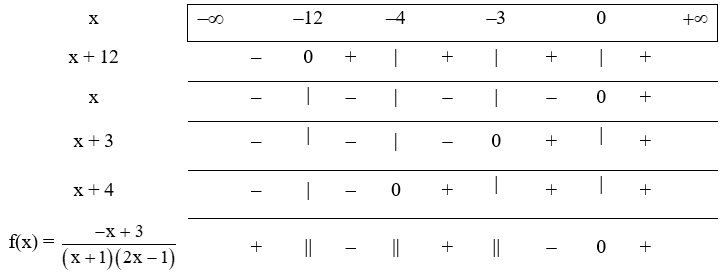
Vậy tập nghiệm của bất phương trình là: S=−12;−4∪−3;0
d)
+ Điều kiện: x2−1≠0⇔x≠±1
+ Ta có:
x2−3x+1x2−1<1⇔x2−3x+1x2−1−1<0
⇔x2−3x+1−x2+1x2−1<0
⇔−3x+2(x−1)(x+1)<0
+ Đặt f(x)=−3x+2(x−1)(x+1)
Ta thấy: f(x) = 0 khi -3x + 2 = 0 suy ra x=23
+ Ta lập bảng xét dấu sau:
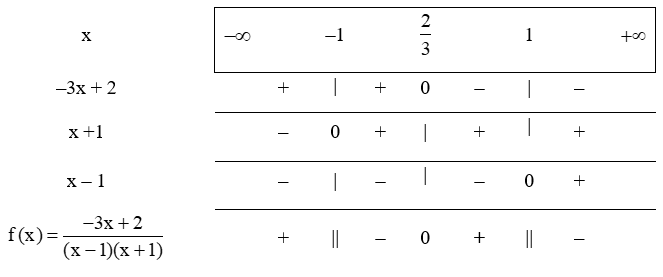
Vậy tập nghiệm của bất phương trình là: S=−1;23∪1;+∞
Xem thêm lời giải bài tập Toán lớp 10 hay, chi tiết khác:
Hoạt động 1 trang 89 Toán 10 Đại số: a) Giải bất phương trình –2x + 3 > 0...
Hoạt động 2 trang 90 Toán 10 Đại số: Xét dấu các nhị thức f(x) = 3x + 2...
Hoạt động 3 trang 92 Toán 10 Đại số: Xét dấu biểu thức f(x) = (2x – 1)(–x + 3)...
Hoạt động 4 trang 92 Toán 10 Đại số: Giải bất phương trình x3 – 4x < 0...
Bài 1 trang 87 Toán 10 Đại số: Xét dấu các biểu thức...
Bài 3 trang 94 Toán 10 Đại số: Giải các phương trình...