|
ĐỀ THAM KHẢO PHÁT TRIỂN MINH HỌA BGD 2024 ĐỀ 5 (Đề gồm có 06 trang) |
KỲ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2024 Bài thi môn: TOÁN Thời gian làm bài: 90 phút, không kể thời gian phát đề |
Họ và tên thí sinh:………………………………………………
Số báo danh:…………………………………………………….
Tiệm cận ngang của đồ thị hàm số đã cho có phương trình là
Số giao điểm của đồ thị hàm số đã cho với trục hoành là
Đường thẳng có đúng ba điểm chung với
là
và
Biết diện tích hình phẳng
là
Giá trị của
bằng
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT
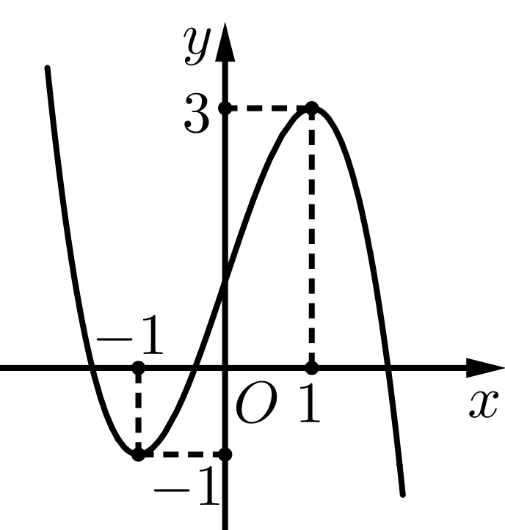
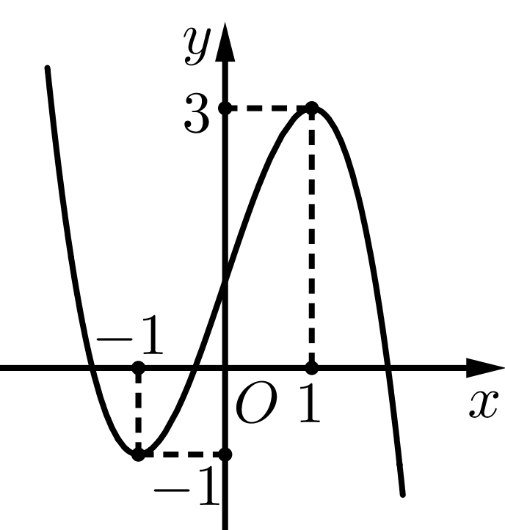
- Cho hàm số
có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng:
A. . B.
. C.
. D.
.
Lời giải
Giá trị cực đại của hàm số là .
- Cho hàm số
. Khẳng định nào dưới đây đúng?
A. . B.
.
C. . D.
.
Lời giải
Chọn D
Có: .
- Tập nghiệm của phương trình
là :
A. B.
C.
D.
Lời giải
Chọn B
- Trong không gian
, cho hai điểm
và
. Vectơ
có tọa độ là
A. B.
C.
D.
Lời giải
Chọn C
hay
.
- Cho đồ thị hàm số
như hình bên. Khẳng định nào sau đây là đúng?
Tiệm cận ngang của đồ thị hàm số đã cho có phương trình là
A. . B.
. C.
. D.
.
Lời giải
Chọn C
Từ đồ thị hàm số ta có tiệm cận ngang có phương trình và tiệm cận đứng có phương trình
.
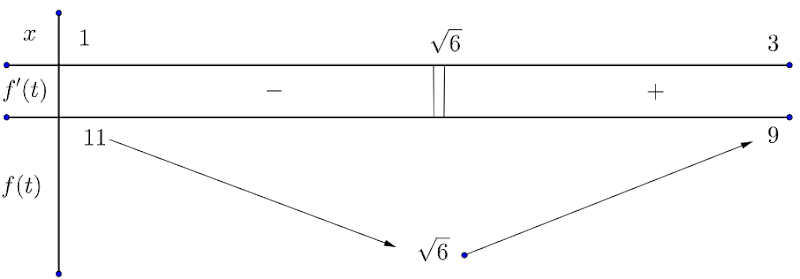
- Hàm số nào dưới đây có bảng biến thiên như sau:
A. B.
C.
D.
Lời giải
Chọn D
Hàm số có bảng biến thiên như trên, trong 4 đáp án đã cho phải là hàm bậc ba với
Do đó ta chọn đáp án D.
- Tập xác định của hàm số
là
A. . B.
. C.
. D.
Lời giải
Chọn B
Hàm số xác định
Tập xác định
- Trong không gian
, vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc tọa độ
và điểm
?
A. . B.
. C.
. D.
.
Lời giải
Chọn D
Đường thẳng đi qua gốc tọa độ và điểm
nhận
là một vectơ chỉ phương.
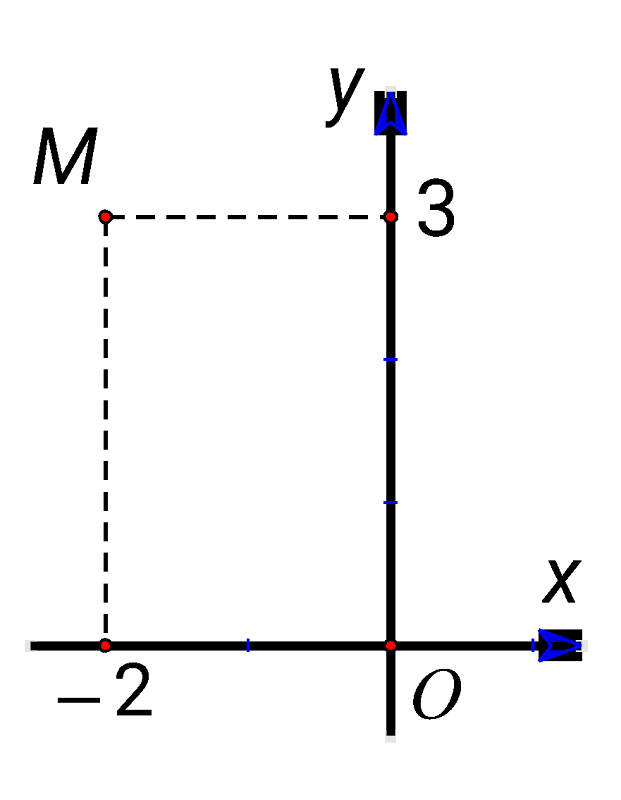
- Điểm
trong hình vẽ bên dưới biểu thị cho số phức
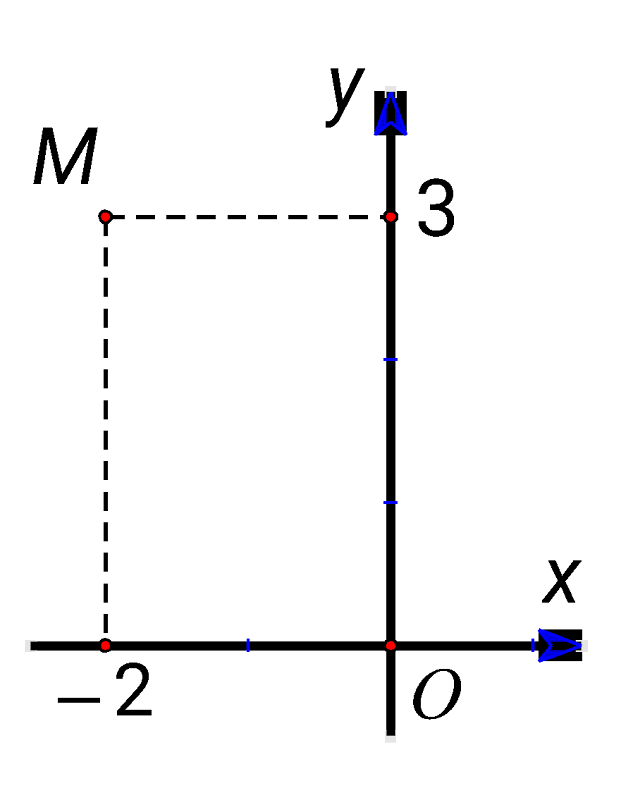
A. B.
C.
D.
Lời giải
Điểm biểu thị cho số phức
- Trong hệ trục tọa độ
, phương trình mặt cầu tâm
bán kính
là:
A. . B.
.
C. . D.
.
Lời giải
Phương trình mặt cầu tâm bán kính
có hai dạng:
Chính tắc:
Tổng quát: .
Vậy đáp án đúng là B.
- Với
là số thực dương tùy ý,
bằng
A. . B.
. C.
. D.
.
Lời giải
Ta có
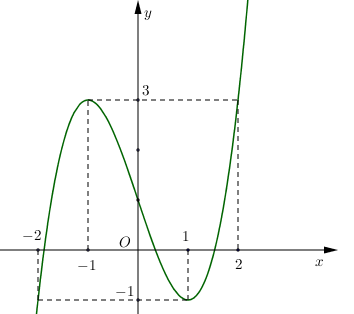
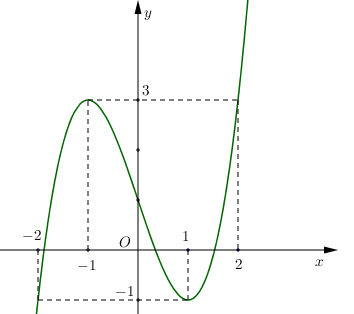
- Cho hàm số
có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào dưới đây
A. . B.
. C.
. D.
.
Lời giải
- Cho khối lăng trụ có diện tích đáy là
, chiều cao là
. Thể tích của khối lăng trụ đã cho bằng
A. . B.
. C.
. D.
.
Lời giải
Thể tích khối lăng trụ: .
- Tập nghiệm của bất phương trình
là
A. . B.
. C.
. D.
.
Lời giải
.
Vậy tập nghiệm của bất phương trình là
.
- Hàm sô nào dưới đây đồng biến trên
A. . B.
. C.
. D.
.
Lời giải
Vì hàm số lôgarit đồng biến trên tập xác định của nó khi cơ số
thỏa mãn
.
- Trong không gian
, cho mặt phẳng
có phương trình là
. Vec-tơ pháp tuyến của mặt phẳng
là
A. . B.
. C.
. D.
.
Lời giải
Phương trình mặt phẳng .
Suy ra một vec-tơ pháp tuyến của mặt phẳng là
.
- Cho hàm số
có đạo hàm
,
. Số điểm cực trị của hàm số đã cho là
A. . B.
. C.
. D.
.
Lời giải
Xét phương trình
Ta có bảng xét dấu
Từ bảng xét dấu ta có số điểm cực trị của hàm số đã cho là .
- Cho hàm số
có đạo hàm trên đoạn
,
và
. Tích phân
bằng
A. . B.
. C.
. D.
.
Lời giải
.
- Biết
và
, khi đó
bằng
A. 3. B. . C.
. D.
.
Lời giải
Ta có: .
- Cho hình chóp tứ giác
có đáy
là hình vuông cạnh
, cạnh bên
vuông góc với mặt phẳng đáy và
. Tính thể tích khối chóp
A. B.
C.
D.
Lời giải
.
- Cho hai số phức
và
. Số phức
bằng
A. . B.
. C.
. D.
.
Lời giải
Ta có
- Một hình nón có diện tích xung quang bằng
và bán kính đáy
thì có độ dài đường sinh bằng
A. . B.
. C.
. D.
Lời giải
Ta có .
- Có bao nhiêu cách xếp
người Việt Nam,
người Pháp và
người Mỹ ngồi lên một chiếc ghế dài gồm
vị trí?. Biết những người cùng quốc tịch phải ngồi gần nhau.
A. . B.
. C.
. D.
.
Lời giải
Xếp người Việt Nam có
cách.
Xếp người Pháp có
cách.
Xếp người Mỹ có
cách.
Xếp vị trí cho người Việt Nam, Pháp, Mỹ có cách.
Vậy có cách.