ĐỀ THAM KHẢO	KỲ THI TỐT NGHIỆP THPT QUỐC GIA NĂM 2024
PHÁT TRIỂN MINH HỌA BGD 2024	Bài thi môn: TOÁN
(Đề gồm có 06 trang)	Thời gian làm bài: 90 phút, không kể thời gian phát đề

Họ và tên thí sinh:………………………………………………

Số báo danh:…………………………………………………….

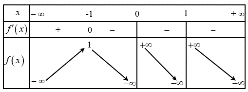
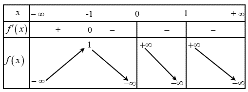
Câu 1:        Cho hàm số  có bảng biến thiên như sau

Giá trị cực đại của hàm số đã cho bằng

A. .        B. .        C. .        D. .

Câu 2:        Cho . Tích phân  bằng

A.         B.         C.         D. 

Câu 3:        Với  là số thực dương bất kì, mệnh đề nào dưới đây đúng?

A.         B. .        C. .        D. .

Câu 4:        Trong không gian , véc tơ nào dưới đây có giá song song hoặc trùng với trục ?

A. .        B. .        C. .        D. .

Câu 5:        Cho hàm số có đồ thị như hình vẽ bên. Đường tiệm cận ngang của đồ thị hàm số có phương trình 

A. .        B.  .        

C.  .        D.  .

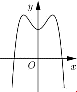
Câu 6:        Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. .        B. .        C. .        D. .

Câu 7:        Tập nghiệm của bất phương trình  là

A. .        B. .        C. .        D. .

Câu 8:        Trong không gian mặt phẳng  đi qua điểm nào dưới đây?

A.         B. .        C. .        D. .

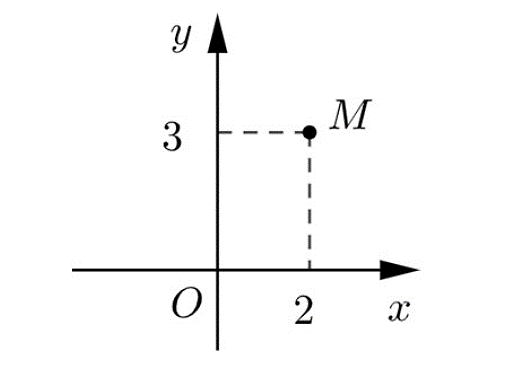
Câu 9:        Trong mặt phẳng tọa độ, cho điểm là điểm biểu diễn số phức như hình vẽ sau:

Phần thực của số phức  bằng

A. .        B. .        C. .        D. .

Câu 10:        Trong không gian , mặt cầu  có diện tích bằng

A. .        B. .        C. .        D. .

Câu 11:        Cho  và là hai số thực dương thỏa mãn . Giá trị của biểu thức  bằng

A. .        B. .        C. .        D. .

Câu 12:        Cho hàm số  có đồ thị như hình vẽ dưới đây.

Hàm số  đồng biến trên khoảng nào?

A. .        B. .        C. .        D. .

Câu 13:        Cho hình nón có diện tích xung quanh bằng  và bán kính đáy bằng . Độ dài đường sinh của hình nón là

A. .        B. .        C. .        D. .

Câu 14:        Các số thực  tùy ý thỏa mãn . Giá trị của  bằng

A. .        B. .        C. .        D. .

Câu 15:        Hàm số nào trong các hàm số sau đây nghịch biến trên ?

A. .        B. .        C. .        D. .

Câu 16:        Trong không gian , cho hai điểm . Tọa độ trung điểm của  là:

A. .        B. .        C. .        D. .

Câu 17:        Cho hàm số  có đạo hàm  Số điểm cực trị của đồ thị hàm số  là

A. 0.        B. 2.        C. 3.        D. 1.

Câu 18:        Họ nguyên hàm của hàm số  là

A. .        B. .        C. .        D. .

Câu 19:        Nếu  thì  bằng

A. .        B. .        C. .        D. .

Câu 20:        Khối chóp tứ giác  có đáy là hình vuông cạnh bằng ,  đều và nằm trong mặt phẳng vuông góc với đáy có thể tích bằng

A. .        B. .        C. .        D. .

Câu 21:        Các số thực  thoả mãn  là:

A. .        B. .        C. .        D. .

Câu 22:        Cho hình nón có diện tích xung quanh bằng  và bán kính đáy . Độ dài đường sinh của hình nón bằng

A. .        B. .        C. .        D. .

Câu 23:        Có bao nhiêu cách chọn một học sinh nam và một học sinh nữ từ một nhóm gồm 7 học sinh nam và 8 học sinh nữ

A. .        B. .        C. .        D. .

Câu 24:        Biết  là một nguyên hàm của hàm số  và . Giá trị của  bằng

A.         B. .        C. .        D. .

Câu 25:        Hàm số  có bảng biến thiên như sau:

Phương trình  có bốn nghiệm thực phân biệt khi và chỉ khi

A. .        B. .        C. .        D. .

Câu 26:        Cho hình trụ có diện tích xung quanh bằng  và độ dài đường sinh bằng đường kính của đường tròn đáy. Bán kính  của hình trụ đã cho bằng

A. .        B. .        C. .        D. .

Câu 27:        Cấp số cộng  hữu hạn có số hạng đầu , công sai  và số hạng cuối là . Cấp số cộng đã cho có bao nhiêu số hạng

A. .        B. .        C. .        D. .

Câu 28:        Gọi ,  là hai nghiệm phức của phương trình  với  có phần ảo âm. Giá trị của  bằng

A. .        B. .        C. .        D. .

Câu 29:        Cho số phức  thỏa mãn . Mô đun của  bằng:

A. .        B. .        C. .        D. .

Câu 30:        Cho hình lập phương . Tính góc giữa hai đường thẳng  và 

A. .        B. .        C. .        D. .

Câu 31:        Cho hình chóp  có , đáy  là hình chữ nhật, biết Khoảng cách từ  đến  bằng:

A. .        B. .        C. .        D. .

Câu 32:        Hàm số liên tục trên và có đạo hàm . Hàm số nghịch biến trên khoảng

A. .        B. .        C. .        D. .

Câu 33:        Từ một hộp chứa  viên bi xanh,  viên bi đỏ và  viên bi vàng; lấy ngẫu nhiên đồng thời viên bi. Xác suất để lấy được  viên bi khác màu bằng

A. .        B. .        C. .        D. .

Câu 34:        Nếu  thì  bằng

A.         B.         C.         D. 

Câu 35:        Giá trị lớn nhất của hàm số  trên  là

A. .        B. .        C. .        D. .

Câu 36:        Với , biểu thức  bằng

A. .        B. .        C. .        D. .

Câu 37:        Trong không gian với hệ tọa độ , mặt cầu  cắt mặt phẳng  theo giao tuyến là một đường tròn có bán kính bằng

A. .        B. .        C. .        D. .

Câu 38:        Trong không gian , viết phương trình đường thẳng  đi qua  và vuông góc với mặt phẳng ?

A. .        B. .        C. .        D. .

Câu 39:        Biết  và  là hai số thực thoả mãn . Giá trị của  bằng

A. .        B. .        C. .        D. .

Câu 40:        Gọi  là tập tất cả các giá trị nguyên của tham số  để hàm số  đồng biến trên khoảng . Tổng các phần tử của  là:

A. .        B. .        C. .        D. .

Câu 41:        Cho hàm số  là hàm bậc bốn có đồ thị như hình bên. Khi diện tích hình phẳng giới hạn bởi đồ thị hai hàm số và  bằng  thì  bằng:

A. .        B. .        C. .        D. .

Câu 42:        Cho số phức  thỏa mãn và  là số thực âm. Giá trị của  bằng

A. .        B. .        C. .        D. .

Câu 43:        Cho hình lăng trụ  có đáy  là tam giác vuông tại , cạnh  và . Biết tứ giác  là hình thoi có  là góc nhọn, mặt phẳng  vuông góc với , góc giữa hai mặt phẳng  và  bằng . Thể tích khối lăng trụ  bằng

A. .        B. .        C. .        D. .

Câu 44:        Trong không gian , cho mặt cầu có phương trình  cắt trục  tại 2 điểm . Tọa độ trung điểm của đoạn  là:

A.         B.         C.         D. 

Câu 45:        Cần bao nhiêu thuỷ tinh để làm một chiếc cốc hình trụ có chiều cao bằng  đường kính đáy bằng  (tính từ mép ngoài cốc), đáy cốc dày  thành xung quanh cốc dày  (tính gần đúng đến hai chữ số thập phân)?

A. .        B. .        C. .        D. .

Câu 46:        Cho các số thực dương  thỏa mãn . Tìm giá trị lớn nhất của biểu thức .

A. .        B. .        C. .        D. .

Câu 47:        Xét các số phức  và  thỏa mãn , . Giá trị nhỏ nhất của biểu thức

 bằng thuộc khoảng nào sau đây?

A. .        B. .        C. .        D. .

Câu 48:        Cho hai đường tròn  và  cắt nhau tại hai điểm ,  sao cho  là một đường kính của đường tròn . Gọi  là hình phẳng được giới hạn bởi hai đường tròn. Quay  quanh trục  ta được một khối tròn xoay. Tính thể tích  của khối tròn xoay được tạo thành.

A.         B.         C.         D. 

Câu 49:        Cho hàm số có đạo hàm là . Có bao nhiêu giá trị nguyên dương của tham số  để hàm số  có đúng cực trị?

A. .        B. .        C. .        D. .

Câu 50:        Trong không gian với hệ trục toạ độ , cho mặt phẳng  và mặt cầu . Một khối hộp chữ nhật  có bốn đỉnh nằm trên mặt phẳng  và bốn đỉnh còn lại nằm trên mặt cầu . Khi  có thể tích lớn nhất, thì mặt phẳng chứa bốn đỉnh của  nằm trên mặt cầu  là . Giá trị  bằng:

A. .        B. .        C. .        D. .

--------------------HẾT--------------------

BẢNG ĐÁP ÁN

1.B	2.A	3.C	4.A	5.B	6.A	7.B	8.A	9.C	10.A
11.C	12.D	13.B	14.A	15.C	16.D	17.D	18.A	19.B	20.C
21.B	22.C	23.D	24.D	25.C	26.C	27.B	28.D	29.A	30.C
31.D	32.C	33.D	34.D	35.C	36.C	37.C	38.C	39.C	40.A
41.A	42.D	43.C	44.A	45.B	46.D	47.A	48.D	49.C	50.B

HƯỚNG DẪN GIẢI CHI TIẾT

Câu 1:        Cho hàm số  có bảng biến thiên như sau

Giá trị cực đại của hàm số đã cho bằng

A. .        B. .        C. .        D. .

Lời giải

Từ bảng biến thiên ta thấy giá trị cực đại của hàm số bằng .

Câu 2:        Cho . Tích phân  bằng

A.         B.         C.         D. 

Lời giải

Ta có: 

Câu 3:        Với  là số thực dương bất kì, mệnh đề nào dưới đây đúng?

A.         B. .        C. .        D. .

Lời giải

Ta có: 

Câu 4:        Trong không gian , véc tơ nào dưới đây có giá song song hoặc trùng với trục ?

A. .        B. .        C. .        D. .

Lời giải

Véctơ có giá song song hoặc trùng với  nên véc tơ đó cùng phương với véc tơ .

Câu 5:        Cho hàm số có đồ thị như hình vẽ bên. Đường tiệm cận ngang của đồ thị hàm số có phương trình

A. .        B.  .        C.  .        D.  .

Lời giải

Dựa vào đồ thị, đường tiệm cận ngang của đồ thị hàm số là .

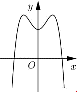
Câu 6:        Đường cong trong hình vẽ bên là đồ thị của hàm số nào dưới đây?

A. .        B. .        C. .        D. .

Lời giải

Dựa vào đồ thị đã cho, ta thấy đồ thị này là đồ thị hàm số bậc 4 có hệ số .

Câu 7:        Tập nghiệm của bất phương trình  là

A. .        B. .        C. .        D. .

Lời giải

Ta có: .

Câu 8:        Trong không gian mặt phẳng  đi qua điểm nào dưới đây?

A.         B. .        C. .        D. .

Lời giải

Thay  vào , ta được: 

Vậy ta có : 

Câu 9:        Trong mặt phẳng tọa độ, cho điểm là điểm biểu diễn số phức như hình vẽ sau:

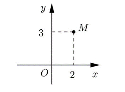
Phần thực của số phức  bằng

A. .        B. .        C. .        D. .

Lời giải

Phần thực của số phức  bằng .

Câu 10:        Trong không gian , mặt cầu  có diện tích bằng

A. .        B. .        C. .        D. .

Lời giải

Mặt cầu  có bán kính . Vậy diện tích mặt cầu  là .

Câu 11:        Cho  và là hai số thực dương thỏa mãn . Giá trị của biểu thức  bằng

A. .        B. .        C. .        D. .

Lời giải

Ta có .

Câu 12:         Cho hàm số  có đồ thị như hình vẽ dưới đây.

Hàm số  đồng biến trên khoảng nào?

A. .        B. .        C. .        D. .

Lời giải

Từ đồ thị hàm số ta thấy hàm số  đồng biến khoảng .

Câu 13:        Cho hình nón có diện tích xung quanh bằng  và bán kính đáy bằng . Độ dài đường sinh của hình nón là

A. .        B. .        C. .        D. .

Lời giải

Diện tích xung quanh của hình nón bằng  trong đó  là độ dài đường sinh và  là bán kính đáy.

Do đó .

Câu 14:        Các số thực  tùy ý thỏa mãn . Giá trị của  bằng

A. .        B. .        C. .        D. .

Lời giải

Ta có: .

Câu 15:        Hàm số nào trong các hàm số sau đây nghịch biến trên ?

A. .        B. .        C. .        D. .

Lời giải

Hàm số  nghịch biến trên  vì .

Câu 16:        Trong không gian , cho hai điểm . Tọa độ trung điểm của  là:

A. .        B. .        C. .        D. .

Lời giải

Ta có tọa độ trung điểm của  là .

Câu 17:        Cho hàm số  có đạo hàm  Số điểm cực trị của đồ thị hàm số  là

A. 0.        B. 2.        C. 3.        D. 1.

Lời giải

Ta có

Mặt khác:  là nghiệm bội lẻ,  là nghiệm bội chẵn nên số điểm cực trị là 1.

Câu 18:        Họ nguyên hàm của hàm số  là

A. .        B. .        C. .        D. .

Lời giải

Ta có 

Câu 19:        Nếu  thì  bằng

A. .        B. .        C. .        D. .

Lời giải

Ta có  .

Câu 20:        Khối chóp tứ giác  có đáy là hình vuông cạnh bằng ,  đều và nằm trong mặt phẳng vuông góc với đáy có thể tích bằng

A. .        B. .        C. .        D. .

Lời giải

Gọi  là trung điểm của .

Theo giả thiết ta có .

Vì  đều có cạnh bằng  nên .

Vậy 

Câu 21:        Các số thực  thoả mãn  là:

A. .        B. .        C. .        D. .

Lời giải

Ta có: .

Câu 22:        Cho hình nón có diện tích xung quanh bằng  và bán kính đáy . Độ dài đường sinh của hình nón bằng

A. .        B. .        C. .        D. .

Lời giải

Ta có . Vậy hình nón có đường sinh .

Câu 23:        Có bao nhiêu cách chọn một học sinh nam và một học sinh nữ từ một nhóm gồm 7 học sinh nam và 8 học sinh nữ